Stiffness Analysis of High Precision Gas Static Pressure Shaft
At present, the precision of precision parts such as automobiles, valves and pumps has reached micron and sub-micron levels, while the precision of ultra-precision parts such as optics, integrated circuits, inertial devices, and optical communications has reached nanometer and sub-nanometer levels. Therefore, the precision and processing capability of the manufacturing equipment must be increased as the accuracy requirements of the parts are improved. For example, precision cutting should achieve the current precision of grinding, and ultra-precision cutting can achieve nanometer and sub-nanometer precision, which can meet the processing requirements of current and future precision ultra-precision parts more economically and efficiently. The core problem of processing equipment is that it should have a high stiffness and high precision rotary shafting and motion mechanism. At present, the higher precision shafting system is a gas static pressure shaft system and a hydrostatic shaft shaft system, but its rigidity is not as good as that of a rolling bearing shaft system, while the precision rolling bearing shaft system has a good rigidity, but its precision is inferior to that of a gas and a liquid static pressure shaft system. This paper discusses the problem of how to improve the stiffness of the gas static shafting.
1 Gas static bearing stiffness
There are many theoretical literatures on porous gas hydrostatic bearings, and many research work has been done on one-dimensional analysis models and two-dimensional analysis and three-dimensional finite element analysis models for gas compressibility, velocity slip, inertial flow correction. Due to the homogenization of the gas film, the porous gas hydrostatic bearing has the advantages of high rotation precision, small friction loss, simple structure, long life and no pollution. The porous gas hydrostatic bearing is widely used in high-precision machine tools and instruments. Germany, France, Japan, the United States and Chinese scholars have conducted a lot of research on it, in order to make greater breakthroughs in its accuracy, stability and rigidity.
The flow of gas in the porous body is generally assumed to be laminar flow, and the flow field of the porous bearing gas film can be calculated according to the Reynolds formula, and the flow of the gas in the porous body follows Darcy's law. As a porous material of a gas static pressure bearing, in addition to its own anisotropy, it may have deformation and partial clogging of material pores due to processing and the like, resulting in a complicated flow state of the fluid therein. To this end, the literature [1] proposed a finite element analysis problem for the static pressure of porous gas. The flow field of the porous bearing gas film can be analyzed using the modified Reynolds formula, which is based on the Darcy formula in the porous flow field. In the overall consideration of finite element analysis of porous bearings, the tangential slip of the gas film, the porous interface and the three-dimensional flow problem in the porous body are considered. A finite element nonlinear equation derived from the airflow field formula solves two problems. Pressure distribution problem in the airflow field. For the classical three-dimensional fluid model, if the lubrication performance of the porous gas hydrostatic bearing is calculated, the corrected Reyn01ds formula is used to calculate the gas film result and the fluid motion in the porous body calculated by the Darcy formula. The finite element analysis method can be used to obtain the gas static bearing stiffness [1] as
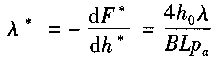
In the formula, the input * and the input are dimensionless static stiffness and static stiffness (N/m), ho, B, L and Pa, respectively. They are the gas film reference thickness (m), the X-direction bearing width (m), the bearing length (m), and the air pressure (Pa). In [2], another physical model of surface pores is proposed: assuming that a layer of dense pores are uniformly distributed on the surface of the porous body, the flow of gas through the thin layer is like obeying a small number of juxtaposed less than L restrictors. Hole flow law. The flow of the rest of the porous layer is still subject to Darcy's law, and complex joint conditions are formed at the joint. Taking the flat plate thrust bearing as an example, the stiffness of the gas static bearing is obtained.
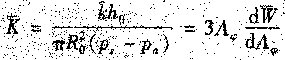
In the formula, φ, K, k, W, Ro, Pa, and Ps are permeability parameters, dimensionless stiffness, gas permeability ratio, load, thrust plate radius, air pressure, and supply pressure, respectively. It can be known from equation (2) that the permeability coefficient into φ has a significant influence on the bearing stiffness, which mainly depends on the gas permeability coefficient φ of the material. Therefore, in the design and manufacture of porous gas hydrostatic bearings, it is necessary to select a gas permeable material that meets the requirements of the gas permeability coefficient φ.
2 Influence of design and manufacturing process on stiffness
Most of the ultra-precision machine tools at home and abroad use gas static pressure bearings as the main shaft shaft system, while the porous gas hydrostatic bearings have higher rigidity. The gas static pressure shaft system generally consists of a pair of aerostatic bearings and a main shaft, where P is the cutting force, y is the total displacement of the main shaft under the force state, X is the deformation curve, and Cl and C2 are the stiffness of the gas static bearing. (figure 1).
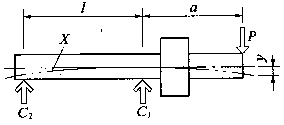
Fig. 1 Schematic diagram of the gas pressure relief shaft system The stiffness of the gas static pressure shaft system consists of the stiffness of the two hydrostatic bearings, the bending stiffness of the main shaft and the contact stiffness of each part. The calculation of the stiffness of the shafting only considers the spindle deflection y and the spindle displacement y2 caused by the deformation of the static pressure film. The total displacement of the main shaft is

In the formula, C is the elastic modulus (N/mm 2 ) of the main shaft material, and I is the average bending anti-bending inertia (mm 4 ) of the inner cross section of the main shaft.
It can be known from equation (8) that in addition to the higher stiffness required for the two hydrostatic bearings, in order to ensure the stiffness of the shafting, the following considerations must be made in the design of the shafting: (1) Select a material with a higher modulus of elasticity as the material. Spindle material, pay attention to the depth and hardness of the surface hardened layer during cold and hot processing; (2) to the spindle support span 2 and the length of the spindle extension "to calculate accordingly, the literature [4] [5] This gives the calculation formula.
3 Experiment and analysis
Graphite materials are often used for porous gas hydrostatic bearing materials. Graphite is a regularly stacked crystal of a hexagonal grid layer and is a porous material.
Generally, the diameter of the pores of the graphite material is as follows: the large pore is Φ. 4-2 μm; transition hole is Φ0.02-0.4 μm; capillary pore is Φ1—10 nm
Individual holes are sometimes up to 100 μm in diameter and should be removed when selecting. The permeability coefficient into φ has a significant effect on the stiffness of the gas static bearing. The permeability coefficient into φ depends mainly on the gas permeability coefficient φ of the material. For graphite materials, no matter whether the diameter of the material pores is too large or too small, a complex gas flow will be formed, which will affect the stability of the gas static pressure characteristics. Therefore, according to formula (2), the graphite material microporous control technology is used to control the excessively large and too small pores of the graphite material.
Equations (1) and (2) are two mathematical models for gas static thrust bearings. Equation (1) is obtained by using the modified Reynolds formula for the flow field of the porous bearing gas film, and Equation (2) is obtained by the finite element analysis method. According to the formula (1) and formula (2), the stiffness and related parameters of the gas static bearing are theoretically analyzed. On this basis, the relationship between the film thickness and the bearing capacity is tested. The test piece is made of graphite material air floating block, the material diameter is 60mm, the thickness is 15mm, the gas permeability coefficient φ is 1.2xl0 -12 m 2 , and the gas supply pressure is 0.5MPa. Figure 2 is a test curve of bearing and film thickness. Through the curvature analysis of the test curve, the film thickness is 160-280 N at 15-30 μm, and the stiffness of the gas static bearing test piece is 14±4 N/μm.
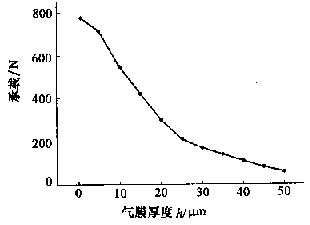
Figure 2 Bearing and film thickness test

Figure 3 Stiffness vs. Spindle Span
According to formula (8) and literature [4] [5], the stiffness of the gas static pressure shaft system was simulated and analyzed. The material E=230x10 3 N/mm 2 and the gas film thickness of 20μm were selected to obtain the stiffness and spindle support span. The relationship curve.
The spindle material, structure, support span, extension length and hot and cold processing were analyzed. The gas static pressure uranium bearing material is made of graphite material, and the spindle material is made of GCrl5, and a set of shafting system is trial-produced. The main parameters of the main shaft structure are: support span l=450mm, extension length a=240mm. The gas static pressure shaft system has been tested to have a stiffness of 280 N/μm. In addition, in the actual design, the design of the rigidity of the machining process and other technical requirements will be comprehensively designed.
4. Conclusion
Porous gas hydrostatic bearings have the advantages of high precision, high stiffness, low friction, no pollution, and are the preferred bearings for micron and nanoscale processing and inspection equipment. In this paper, the analysis method of 7 high-precision gas static pressure shaft stiffness is discussed from the aspects of porous gas static bearing stiffness and spindle geometry design principle, and it has been applied in engineering. It is proved that the graphite high-precision gas static pressure shaft system is not only high in precision but also high in rigidity. There is still much work to be done on high-precision and high-rigidity shafting, such as the development of new materials for porous gas hydrostatic bearings, the standardization of gas static pressure shafts for internal motors, high-precision, high-stiffness magnetic gas static pressure shafting, advanced The throttling method, etc., will carry out the work of precision engineering.
Customized Telescopic Tube,Pvc Square Telescopic Tube,Black Telescopic Tube,Rectangle Telescopic Tube
Wuxi Jierui Changkun New Material Technology Co., Ltd , https://www.jrck-plastic.com